分離公理

Illustrations of the properties of Hausdorffness, regularity and normality — 某些分離公理的圖示。藍色區塊代表一個開集，紅色方塊代表一個閉集，且黑色圓圈則代表一點。

在拓撲學及相關的數學領域裡，通常對於所討論的拓撲空間加有各種各樣的限制條件，分離公理即是指之中的某些限制條件。這些分離公理有時候被叫做吉洪諾夫分離公理，得名於安德烈·尼古拉耶維奇·吉洪諾夫。部分分離公理以字母T開頭，是由德文單詞「Trennung」而來，意義是分離。

分離公理之所以稱為公理，是因為以前定義拓撲空間時，有些人會將其也做為公理來定義，而得出較現在意思狹義的拓撲空間。但在拓撲空間的公理化完成後，那些都成了「各種」的拓撲空間。然而，「分離公理」這一詞就這樣固定了下來。

初步定義[編輯]

在定義分離公理之前，讓我們先了解在拓撲空間中，可分離的集合(和點)的具體含意。（須注意的是，可分離的集合不一定等同於下一節所定義的「分離空間」。）

分離公理是利用拓撲的方法來分辨不相交的集合及相區別的點。不只要拓撲空間內的元素是相區別的，更要這些元素是「拓撲可區別的」；不只要拓撲空間內的子集是不相交的，更要這些子集是（以某種方式）「可分離的」。分離公理聲稱，無論如何，若點或集合在某些較弱意思下是可區別的或可分離的，也必須在某些較強的意思下是可區別或可分離的。

設 $X$ 為一拓撲空間， $A,B\subseteq X$ ， $\mathbb {R}$ 是實數集，定義：

拓撲可區分: $A,B$ 稱為拓撲可區分的，若且唯若 $A,B$ 的鄰域系 $U(A)$ 和 $U(B)$ 不相等（即，存在某個 $A$ 的鄰域，不是 $B$ 的鄰域，或反之）。
可分離: $A,B$ 稱為可分離的，若且唯若 $A\cap {\bar {B}}$ 和 ${\bar {A}}\cap B$ 都為空。（ ${\bar {A}}$ 是 $A$ 的閉包）。注意： ${\bar {A}}\cap {\bar {B}}$ 可以不為空。
鄰域可分離: $A,B$ 稱為鄰域可分離的，若且唯若存在 $A$ 的鄰域 $U$ 和 $B$ 的鄰域 $V$ ，使得 $U\cap V$ 為空。
閉鄰域可分離: $A,B$ 稱為閉鄰域可分離的，若且唯若存在 $A$ 的閉鄰域 $U$ 和 $B$ 的閉鄰域 $V$ ，使得 $U\cap V$ 為空。
函數可分離: $A,B$ 稱為函數可分離的，若且唯若存在連續函數 $f:X\to \mathbb {R}$ ，使得 $f(A)=\{0\}$ ， $f(B)=\{1\}$ 。
函數完全分離: $A,B$ 稱為函數完全分離的，若且唯若存在連續函數 $f:X\to \mathbb {R}$ ，使得 $f^{-1}(\{0\})=A$ ， $f^{-1}(\{1\})=B$ 。

對於 $X$ 中的點 $x,y$ （或點 $x$ 和子集 $A$ ），稱它們為拓撲可分，可分離，鄰域可分離等等，若且唯若單元素集合 $\{x\}$ 和 $\{y\}$ （或 $\{x\}$ 和子集 $A$ ）是拓撲可分，可分離，鄰域可分離等等。

以上這些條件是按強度依序給出的：任何兩個拓撲可區分的點也必然是相區分的，任何兩個分離的點也必然是拓撲可區分的。更進一步地說，任何兩個可分離的集合也必然是不相交的，任何兩個領域上可分離的集合也必然是可分離的，以此類推。

上述條件更詳細的敘述(包括分離公理外的用途)，請參見分離集合和拓撲不可區分性等條目。

主要定義[編輯]

下面的定義都會直接使用到上面的初步定義。

大部份的分離公理都會有另一個等價的定義。下面所給出的定義會維持一致的模式，以和上一節所定義的許多分離的概念相連結。其他等價的定義則分別寫在個別的條目之中。

在下面所有的定義之中，X是一個拓撲空間，所有的函數都假設為連續的。

X稱為T₀空間或「柯爾莫果洛夫空間」，若在X內，任意兩個相區別的點皆為拓撲可區分的。

X稱為R₀空間或「對稱空間」，若在X內，任意兩個拓撲可區分的點都是可分離的。

X稱為T₁空間、「可及空間」或「弗雷歇空間」，若在X內，任意兩個相區別的點都是可分離的。X為T₁空間，若且唯若X同時為T₀及R₀空間。

X稱為R₁空間或「預正則空間」，若在X內，任意兩個拓撲可區分的點都是鄰域上可分離的。R₁空間必然也是R₀空間。

X稱為T₂空間或「豪斯多夫空間」，若在X內，任意兩個相區別的點都是鄰域上可分離的。X為豪斯多夫空間，若且唯若X同時為T₀及R₁空間。豪斯多夫空間必然也是T₁空間。

X稱為T_2½空間或「烏雷松空間」，若在X內，任意兩個相區別的點都是閉鄰域上可分離的。T_2½空間必然也是豪斯多夫空間。

X稱為完全豪斯多夫空間或「完全T₂空間」，若在X內，任意兩個相區別的點都是函數上可分離的。完全豪斯多夫空間必然也是T_2½空間。

X稱為正則空間，若在X內，給定一點x及一閉集F，則若x不屬於F，x和F即為鄰域上可分離的（實際上，在一個正則空間裡，x和F也同樣會是閉鄰域上可分離的）。正則空間必然也是R₁空間。

X稱為正則豪斯多夫空間或「T₃空間」，若X同時為T₀及正則空間。正則豪斯多夫空間必然也是T_2½空間。

X稱為完全正則空間，若在X內，給定一點x及一閉集F，則若x不屬於F，x和F即為函數上可分離的。完全正則空間必然也是正則空間。

X稱為吉洪諾夫空間、「T_3½空間」、「完全T₃空間」或「完全正則豪斯多夫空間」，若X同時為T₀及完全正則空間。吉洪諾夫空間必然同時也是正則豪斯多夫空間及完全豪斯多夫空間。

X稱為正規空間，若在X內，任意兩個相區別的閉子集都是鄰域上可分離的（實際上，在正規空間裡，任意兩個相區別的閉子集也同樣會是函數上可分離的；這稱為烏雷松引理）。

X稱為正規豪斯多夫空間或「T₄空間」，若X同時為T₁及正規空間。正規豪斯多夫空間必然同時也是吉洪諾夫空間及正規正則空間。

X稱為完全正規空間，若在X內，任意兩個相區別的子集都是鄰域上可分離的。完全正規空間必然也是正規空間。

X稱為完全正規豪斯多夫空間、「T₅空間」或「完全T₄空間」，若X同時為完全正規及T₁空間。完全正規豪斯多夫空間必然也是正規豪斯多夫空間。

X稱為完美正規空間，若在X內，任意兩個相區別的閉子集都是函數上完全分離的。完美正規空間必然也是完全正規空間。

X稱為完美正規豪斯多夫空間、「T₆空間」或「完美T₄空間」，若X同時為完美正規及T₁空間。完美正規豪斯多夫空間必然也是完全正規豪斯多夫空間。

各空間之間的關係[編輯]

T₀空間很特別，因為它不只可以當做一個性質加在其他空間上（如完全正則空間加上T₀即為吉洪諾夫空間），也可以由某個空間中刪去此一性質（如豪斯多夫空間刪去T₀即為R₁空間）；更多資訊請見柯爾莫果洛夫商空間。當其應用在分離公理時，便會導致如下表所列的關係：

T₀版本	無T₀版本
T₀	－
T₁	R₀
豪斯多夫(T₂)	R₁
T_2½	無給定名稱
完全豪斯多夫	無給定名稱
正則豪斯多夫(T₃)	正則
吉洪諾夫(T_3½)	完全正則
正規T₀	正規
正規豪斯多夫(T₄)	正規正則
完全正規T₀	完全正規
完全正規豪斯多夫(T₅)	完全正規正則
完美正規T₀	完美正規
完美正規豪斯多夫(T₆)	完美正規正則

在表中，利用柯爾莫果洛夫商空間運算，右邊的空間加上T₀即為左邊的空間，左邊的空間刪去T₀即為右邊的空間。

除了T₀的加上及刪去之外，各空間之間的關係則可由下圖指明出來：

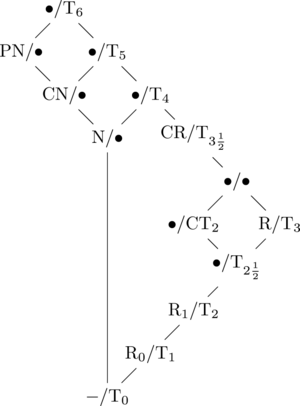
在圖中，無T₀版本的空間在斜線的左邊，T₀版本的空間則在斜線的右邊。之中的字母代表的意思： P為完美（perfectly）、C為完全（completely）、N為正規（normal）、R為正則（regular）。黑點代表該空間沒有給定名稱。

結合兩個空間的性質最後會產生的空間可由上圖得知，只要看兩點向上的分支會交會在哪一點即可。例如，若有一個空間同時為完全正規（CN）及完全豪斯多夫（CT₂）空間，則查看兩點向上的分支，會發覺為「•/T₅」。因為完全豪斯多夫空間為斜邊的T₀端（即使完全正規空間不是），最後得到的空間便會在斜邊的T₀端。亦即，完全正規完全豪斯多夫空間即為T₅空間。

再看一次上圖，正規空間及R₀空間結合在一起，由於會經過許多右側的分支，也意指會產生許多兩個空間所沒有的其他性質。因為正則性是之中最為人知的性質，結合正規空間及R₀空間而成的空間一般稱為「正規正則空間」。基於類似的想法，正規T₁空間通常稱為「正規豪斯多夫空間」。上述的慣用名稱可以延伸至其他正則空間與豪斯多夫空間之上。

參考文獻[編輯]

Michael C. Gemignani; Elementary Topology; ISBN 0486665224
Schechter, Eric; 1997; Handbook of Analysis and its Foundations; Publisher: Academic Press; https://web.archive.org/web/20150307061351/http://www.math.vanderbilt.edu/%7Eschectex/ccc/
- 包含 R_i 公理（及其他）
Stephen Willard, General Topology, Addison-Wesley, 1970. Reprinted by Dover Publications, New York, 2004. ISBN 0-486-43479-6 (Dover edition).
- 包含本條目除 R_i 以外之公理和定義
There are several other good books on general topology, but beware that some use slightly different definitions.